LC122. 买卖股票的最佳时机 II

题目描述

这是 LeetCode 上的（122. 买卖股票的最佳时机 II） ，难度为 中等。

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示：

• 1 <= prices.length <= 3 * 104
• 0 <= prices[i] <= 104

---

题解

动态规划

• dp[i][j]

  • dp[i][j] 表示第 i 天交易完后的最大利润
  • j 表示是否持有股票

• 动态规划初始状态

  • dp[0][0] = -prices[0]

• 如果当前持有股票

  • 可能前一天持有股票，今天什么都不做
    • dp[i][1] = dp[i-1][1]
  • 可能前一天未持有股票，今天买入股票
    • `dp[i][1] = dp[i-1][0] - prices[i]

• 如果当前未持有股票

  • 可能前一天未持有股票，今天什么都不做
    • dp[i][0] = dp[i-1][0]
  • 可能前一天持有股票，今天卖出股票
    • dp[i][0] = dp[i-1][1] + prices[i]

• 则状态转移方程为

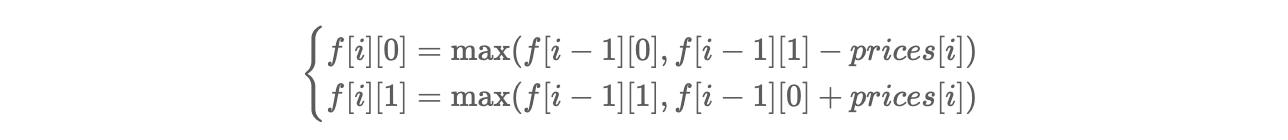
• 最终返回最大利润`dp[len-1][0]

代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        int dp[len][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for (int i = 1; i < len; ++i) {
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        }
        return dp[len - 1][0];
    }
};

复杂度

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

动态规划（空间压缩）

• 第 i 天的状态，只与第 i−1 天的状态有关
• 因此我们可以只用两个变量来维护第 i−1 天的状态
• 从而将空间复杂度优化到 O(1)

代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int dp0 = 0; 
        int dp1 = -prices[0]; 
        for(int i = 0; i < prices.size(); i++){
            int newdp0 = max(dp0, dp1 + prices[i]); 
            int newdp1 = max(dp1, dp0 - prices[i]);
            dp0 = newdp0;
            dp1 = newdp1;
        }
        return dp0;
    }
};

复杂度

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

最后

• 参考了leetcode题解